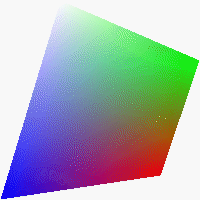
Gouraud Shading

Gouraud shading, also called intensity interpolation, provides a way to display smooth-shaded polygons by defining the RGB color components of each polygon vertex. It operates by first interpolating the RGB values between the vertical vertices along each edge. This gives us the RGB components for the left and right edges of each scan line (pixel row). We then display each row of pixels by horizontally interpolating the RGB values between that row's left and right edges. This produces a remarkably smooth-shaded polygon. Fastgraph supports Gouraud shading for direct color virtual buffers, but not for 256-color virtual buffers.

To illustrate Gouraud shading, consider a polygon with four vertices. Assume its upper left vertex is pure white (RGB = 255,255,255), the upper right vertex is pure green (0,255,0), the lower right vertex is pure red (255,0,0), and the lower left vertex is pure blue (0,0,255). The resulting Gouraud-shaded polygon would look like this:

If all four vertices have the same RGB values, note that a Gouraud-shaded polygon becomes a single-color polygon.

Strictly speaking, Gouraud shading involves not only drawing the shaded polygon, but first determining suitable RGB values for each polygon vertex. Fastgraph's Gouraud shading functions assume that you have already done this first step. Most 3D reference books will describe ways to determine RGB values for the polygon vertices based on ambient lighting, diffuse (directed) lighting, and the surface's reflectance. Then, if you are drawing an object made up of several Gouraud-shaded polygons, for each object vertex you average the RGB components for all polygon vertices that meet at that point. For more details on Gouraud shading, please consult the 3D references listed on http://www.fastgraph.com/books.