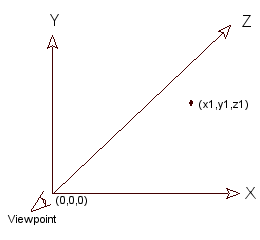 Fig. 1.1 A left-handed 3D coordinate system.
|
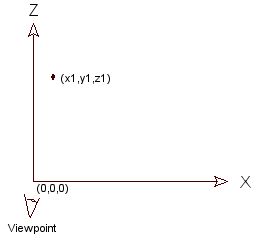 Fig. 1.2 Top down view.
|
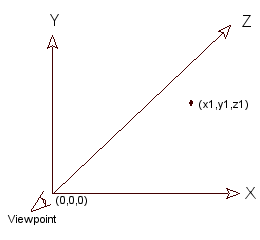 Fig. 1.1 A left-handed 3D coordinate system.
|
 Fig. 1.2 Top down view.
|
Defining Your Point of ViewIn order to draw objects in 3D space, you need to have some way of defining the space you will be working in. Typically, this means you need to think in terms of a left-handed 3D coordinate system as shown above. You should be familiar with the graphical representations of coordinate axes. For our purposes, the X and Z axes will form a plane parallel to the ground, and the Y axis will define a line perpendicular to the ground. So a player walking through a playing field would be considered to be at some position in the XZ plane, and the distance between his head and his feet would be defined in terms of Y. This is by no means the only way to position a game element in a 3D coordinate system, but it is common, and this is the convention we will use in this discussion. We are using a left-handed coordinate system, which means the positive Z axis points away from the user's eyes, or "into" the screen. Take note of the point of view, also known as the POV or "viewpoint". The POV simply defines where you are, and in what direction you are looking. In 3D space, you can be anyplace, and look in any direction. In the pictures above, notice you are at the origin and you are looking down the Z axis. We will call this the default viewpoint. You can change the viewpoint in Fastgraph quite easily with fg_3dpov().fg_3Dpov (0,0,0,0,0,0).
If you want to rotate your viewpoint that you are looking down the positive X
axis, set the values like this: fg_3Dpov (0,0,0,0,900,0).
That means you have rotated by 90 degrees
in a clockwise direction around the Y axis. See Figure 1.3.
|
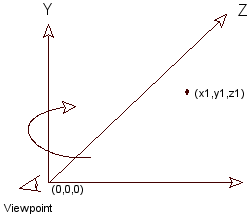 Figure 1.3 Rotating the viewpoint around the Y axis.
|
|
If you forget to call fg_3Dpov() in your program, Fastgraph will
assume the default viewpoint. A game like a first-person shooter (FPS),in which
the player's point of view is constantly changing, will call the fg_3Dpov()
function many times, perhaps as often as once per frame.
Defining Your World
Let's think about how big things should be. Since 3D coordinate systems are imaginary,
they can represent anything you want. It doesn't matter how big your world is, what
matters is how things are proportioned with respect to each other. You need to give
this a little thought in order to avoid an Alice in Wonderland effect -- houses too
small to fit in or bottles too large to drink out of.
It might be easiest if we start with a familiar object and measure it. Suppose you
are writing a 3D game that involves walking through rooms and corridors. Pick an
object that might be in a room, for example a chair. How tall is it? Suppose your
chair is about three feet high. When you walk into the room, you want the size of the
room to be proportionate to the size of the chair. Perhaps your chair is in a room
that is 20 feet long by 20 feet wide. If you define your room to be 20x20, and you
define your chair to have a height of 3, they will probably fit together reasonably
well and look natural.
Now think about where you want to put your origin. It can go anywhere. It doesn't
matter. Everything else in the world will have coordinates relative to the origin.
But there is nothing mysterious about that, it is just distances in the X, Y, and
Z planes. For our purposes, let's put the origin in the center of the room with
the chair.
Now, let's think about the objects you will see on the screen. How big are they?
How close do you need to be to the chair in order for it to fill the whole screen?
How far away will you be when the chair fills up only one tenth of your screen?
You can use Fastgraph's fg_3Dviewport() to establish the extents of the viewport,
and the ratio of objects in your world to their image on the screen.
Suppose you want your viewing area to be 640 pixels wide and 480 pixels high. Call
fg_3Dviewport like this:
The Extents of Your VisionNow, let's consider how objects in your 3D coordinate system will appear on your screen. The fg_3Dviewport() function described earlier describes how big the image will be on the screen. But how big will the objects in it appear?The easiest way to understand it is to consider that when the ratio is one, objects have a width equal to their distance from the screen. That is, if an object is 10 feet wide, and it is 10 feet away from you, it will fill the entire screen. See Figure 1.4.
|
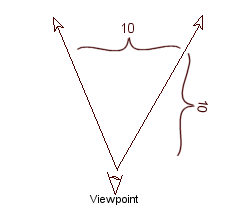 Fig. 1.4 Your angle of vision.
|
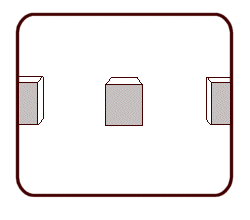 Fig. 1.5 What you see on the screen.
|
|
For another example, consider three cubes. Suppose you are at the origin looking
down the Z axis as in Figure 1.1. One cube is centered at (0, 0, 10), or in
other words 10 feet directly in front of you. The second cube is at (-5, 0, 10),
that is 10 feet ahead and 5 feet to the left. The third cube is at (5, 0, 10), or
10 feet ahead of you and 5 feet to the right. So the distance between the centers
of the two outside cubes is 10 feet. Your screen will look something like Figure
1.5. Note that feet is an arbitrary choice of units. It could be 10 inches, 10 miles,
or 10 light years. It would make no difference. Similarly, if the cubes were 5 feet
away and the outer two were 5 feet apart, the screen image would be similar, but
the cubes would appear to be twice as large. In Chapter 3, we will see that using smaller units (inches instead of feet) gives more control over the z clipping limits. In Chapter 6, we will discuss alternative ways of establishing your viewpoint position and orientation.
ReviewSomewhere in the beginning of your program, probably in the Windows' create handler, you are going to need to establish your coordinate system, your screen extents, and your point of view. If you are unsure of what values to use, start with these and experiment.
That is enough to initialize Fastgraph's 3D system. Use these functions in
addition to the regular Fastgraph functions which initialize Fastgraph's virtual
buffers, palettes, and if you desire, DirectDraw or Direct3D immediate mode. See
the Fastgraph manual for more information about those initializations, or just
copy from one of the examples provided later in this tutorial. Now, let
us proceed to a discussion of how to put objects in your 3D space.
|
Introduction
Chapter 1 |
Chapter 2 |
Chapter 3
Chapter 4 |
Chapter 5 |
Chapter 6 |
Chapter 7
Appendix 1 |
Appendix 2 |
Appendix 3
Benchmarks
Fastgraph Home Page
